2022-01-10

最短路問題とポテンシャル

結論

$\displaystyle{ \phi }$ をポテンシャルとして $\displaystyle{ \phi[v] - \phi[s] }$ の最大値を求める問題は、 $\displaystyle{ s }$ を始点として $\displaystyle{ v }$ への最短路長を求める問題の双対問題（dual problem）となる。

前提

線形計画問題（以下 LP ）:

$\displaystyle{ m \times n }$ の行列 $\displaystyle{ A }$
$\displaystyle{ m }$ 次元のベクタ $\displaystyle{ b }$
$\displaystyle{ n }$ 次元のベクタ $\displaystyle{ c }$

が与えられ、 $\displaystyle{ Ax \le b }$ の制約下において、 objective function $\displaystyle{ \sum_{i=1}^{n} c_i x_i }$ を最大化する $\displaystyle{ n }$ 次元のベクタ $\displaystyle{ x }$ を求める問題。

ポテンシャル

以下のグラフを LP で定式化することを考える。

それぞれの辺がどの頂点を繋いでいるのかを表現した $\displaystyle{ |E| \times |V| }$ 行列 $\displaystyle{ A }$ を用意する。辺 $\displaystyle{ (v_i, v_j) }$ について $\displaystyle{ i }$ 列 $\displaystyle{ =-1 }$ , $\displaystyle{ j }$ 列 $\displaystyle{ =1 }$ , それ以外の要素を $\displaystyle{ 0 }$ 埋めして表現する。

さらに、

それぞれの頂点への到達コストを、 $\displaystyle{ |V| }$ 次元のベクタ $\displaystyle{ x }$
それぞれの辺のコスト $\displaystyle{ w(u, v) }$ を、 $\displaystyle{ |E| }$ 次元のベクタ $\displaystyle{ b }$

とする。

これらを元として、このグラフは、次のように定式化することができる。

分解すると次のようになる。

$\displaystyle{ x_1 - x_2 \le 0, }$

$\displaystyle{ x_1 - x_5 \le -1, }$

$\displaystyle{ x_2 - x_5 \le 1, }$

$\displaystyle{ x_3 - x_1 \le 5, }$

$\displaystyle{ x_4 - x_1 \le 4, }$

$\displaystyle{ x_4 - x_3 \le -1, }$

$\displaystyle{ x_5 - x_3 \le -3, }$

$\displaystyle{ x_5 - x_4 \le -3, }$

この制約は何を意味するか。

たとえば、 $\displaystyle{ x_5 - x_4 \le -3 }$ を例とすると、「 $\displaystyle{ v_5 }$ への到達コスト $\displaystyle{ x_5 }$ は、 $\displaystyle{ x_4 }$ に、 $\displaystyle{ v_4 }$ から $\displaystyle{ v_5 }$ への経路のコストを足し合わせたもの $\displaystyle{ x_4 + w(v_4, v_5) }$ 以下になる」ことを意味する。

$\displaystyle{ Ax \le b }$ の制約を満たす $\displaystyle{ x }$ の解の1つに、 $\displaystyle{ x = (-5, -3, 0, -1, -4) }$ が考えられる。

他にも、 $\displaystyle{ x = (0, 2, 5, 4, 1) }$ など、複数の解が考えられるだろう。

この、 $\displaystyle{ Ax \le b }$ の制約を満たす解の組み合わせ、具体的には

任意の $\displaystyle{ u,v \in V }$ に対して、 $\displaystyle{ \phi [v] - \phi [u] \le w(u,v) }$ を満たすような $\displaystyle{ \phi }$

のことを ポテンシャル と呼ぶ。

参考にした書籍でわかりやすかった説明を引用する。

各節点間がピンと張られているとは限らない場合において、各節点の位置関係としてありうるものをポテンシャルと呼びます。より正確には、各頂点 $\displaystyle{ v }$ に対して値 $\displaystyle{ \phi[v] }$ が定まっているとき、任意の辺 $\displaystyle{ e=(u,v) }$ に対して、 $\displaystyle{ \phi[v] - \phi[u] \le w(u,v) }$ を満たすような $\displaystyle{ \phi }$ のことをポテンシャルと呼びます。

最短路問題とポテンシャル

実は、点 $\displaystyle{ u }$ から点 $\displaystyle{ v }$ への最短路（最小コストで到達できる経路）を求める問題は、 $\displaystyle{ \phi[v] - \phi[u] }$ の最大値を求める問題の双対問題（dual problem）となっている。

すなわち、以下の命題が成立する。

頂点 $\displaystyle{ u }$ から頂点 $\displaystyle{ v }$ へ到達可能な時、 $\displaystyle{ u }$ から $\displaystyle{ v }$ への最小コスト $\displaystyle{ = max(\phi[v] - \phi[u]) }$

証明

始点 $\displaystyle{ u }$ から頂点 $\displaystyle{ v }$ への任意の路 $\displaystyle{ P }$ に対して、

$\displaystyle{ w(P) = \sum_{e \in P}{w(e)} \ge \sum_{e \in P}{\phi [e_{to}] - \phi [e_{from}]} = \phi[v] - \phi[u] }$

が成立する。これが任意の路 $\displaystyle{ P }$ 、ポテンシャル $\displaystyle{ \phi }$ に対して成り立つことから、

$\displaystyle{ min\{w[P]\} = max\{\phi[v] - \phi[u]\} }$

となる。

おせわになりました

2021-11-22

ソート

ルールに基づいて並べ替えること。

ソート (英: sort) は、データの集合を一定の規則に従って並べること。日本語では整列（せいれつ）、並べ替え（ならべかえ）、分類（ぶんるい）などと訳される。 https://ja.wikipedia.org/wiki/%E3%82%BD%E3%83%BC%E3%83%88

sortの語源: 古フランス語の sortir （≒sort, assort）より - https://www.etymonline.com/search?q=sort - https://en.wiktionary.org/wiki/sortir

sortの評価指標

計算量
in-place性（追加で必要な外部メモリ容量）
安定性（stability）

in-place性

追加の記憶領域をほとんど使わない性質。

in-placeアルゴリズムとは、計算機科学においてデータ構造の変換を行うにあたって、追加の記憶領域をほとんど使わずに行うアルゴリズムを意味する。 in-place とは「その場で」といった意味であり、入力が出力で上書きされることが多いことから来る用語である。 in-place でないアルゴリズムは not-in-place あるいは out-of-place などと呼ばれることもある。 https://ja.wikipedia.org/wiki/In-place%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0

似た概念に空間計算量がある。

例えば、なんらかの文字列を逆転する関数を考える。

以下の関数 reverse() は、 sort対象である配列 a の他に、同じサイズ $\displaystyle{ n }$ の配列 b を用意している。すなわち、配列 b の領域に $\displaystyle{ O(n) }$ の空間を必要とする。（空間計算量 $\displaystyle{ O(n) }$ とも）。

 function reverse(a[0..n])
     allocate b[0..n]
     for i from 0 to n
         b[n - i] = a[i]
     return b

対して、次の関数 reverse-in-place() は、sort処理が与えられた配列 a で完結しているため、 in-placeであると言える。

 function reverse-in-place(a[0..n])
     for i from 0 to floor(n/2)
         swap(a[i], a[n-i])

安定性

sort対象に同一の値があった時に、元の順序が保たれているかどうか。

具体例:

Goのsort.Slice() は安定ソートではない。 https://play.golang.org/p/Ez6S89OVz4H

Kotlinの collections.sortedBy() は安定ソート。 https://pl.kotl.in/oSm-SmU9m

sortアルゴリズム

挿入ソート

左から $\displaystyle{ i }$ 枚分が整列済みの状態であることを仮定して、 $\displaystyle{ i＋1 }$ 枚目のカードを適切な場所に挿入していくアルゴリズム。

評価

計算量: $\displaystyle{ O(N^2) }$
in-place: true
stable: true

実装例

fn insertion_sort(v: Vec<i32>) -> Vec<i32> {
    let mut v = v;
    for i in 0..v.len() {
        for j in (0..i).rev() {
            if v[j] > v[j+1] {
                v.swap(j, j+1);
            }
        }
    }
    v
}

マージソート

分割統治法によるソート。配列を半分に分割し、左右それぞれを再帰的にソートしておき、その両者を併合することを繰り返す。

併合するときは次のような操作を行う。

左側配列 $\displaystyle{ a[left:mid] }$ と右側配列 $\displaystyle{ a[mid:right] }$ の中身をそれぞれ外部配列にコピー
左側に対応する外部配列と，右側に対応する外部配列がともに空になるまで，「左側の最小値」と「右側の最小値」を比較して小さい方を選び，それを抜き出すことを繰り返す．ただし，左側の外部配列と右側の外部配列のうち，どちらかが空である場合には，他方の最小値を抜き出す．

ここで、図12.4のように、右側の外部配列を左右反転することを考える。

こうすることにより、併合処理において、左側の外部配列または右側の外部配列が空であるかどうかを確認する必要がなくなり、「つないでできた外部配列の両端のうち，小さい方を抜き出すことを繰り返す」という明快なものとなる。

評価

計算量:
- 分割: $\displaystyle{ O(lgN) }$
- 併合: $\displaystyle{ O(N) }$ を $\displaystyle{ O(lgN) }$ 回 = $\displaystyle{ O(NlgN) }$
in-place: false
- 併合するときに外部配列を要する
- そのため、組み込み系などの資源が限られた状況下では採用されづらい
stable: true

実装例

// left, right: 0-index of v
fn merge_sort(v: &mut Vec<i32>, left: usize, right: usize) {
    if right > left {
        let mid = (left + right)/2;
        merge_sort(v, left, mid);
        merge_sort(v, mid+1, right);
        merge(v, left, mid, right);
    }
}

fn merge(v: &mut Vec<i32>, left: usize, mid:usize, right:usize) {
    let left_vec = v[left..=mid].to_vec();
    let right_vec = v[mid+1..=right].to_vec();

    let mut left_itr = left_vec.iter().peekable();
    let mut right_itr = right_vec.iter().peekable();

    for i in left..=right {
        match (left_itr.peek(), right_itr.peek()) {
            (None, Some(_)) => v[i] = *right_itr.next().unwrap(),
            (Some(_), None) => v[i] = *left_itr.next().unwrap(),
            (Some(l), Some(r)) if l < r => v[i] = *left_itr.next().unwrap(),
            (Some(l), Some(r)) if r < l => v[i] = *right_itr.next().unwrap(),
            (Some(_), Some(_)) => v[i] = *left_itr.next().unwrap(),
            _ => break
        }
    }
}

マージソートの計算量について

マージソートの計算量を $\displaystyle{ T(N) }$ とすると、以下の漸化式が成り立つ。

$\displaystyle{ T(N) = \begin{cases} O(1) & (N = 1) \\ 2T(\frac{N}{2}) + O(N) & (N \gt 1) \end{cases} }$

これが $\displaystyle{ T(N) = O(NlgN) }$ となることを示す。

まず、漸化式中に含まれる定数を一般化し、 $\displaystyle{ a,b }$ を $\displaystyle{ a,b \ge 1 }$ を満たす整数、 $\displaystyle{ c,d }$ を正の実数として

$\displaystyle{ T(N) = \begin{cases} c & (N = 1) \\ aT(\frac{N}{b}) + dN & (N \gt 1) \end{cases} }$

と変換する。ここで得られた漸化式の計算量が、

$\displaystyle{ T(N) = \begin{cases} O(N) & (a \lt b) \\ O(NlogN) & (a = b) \\ O(N^{log_ba}) & (a \gt b) \\ \end{cases} }$

となることを見ていく。

$\displaystyle{ N }$ が $\displaystyle{ N = b^k }$ と表される整数である場合について考える。漸化式を繰り返し用いると、

となる。

よって、

冒頭で記した通り、マージソートは次の漸化式で計算量を表すことができ、 $\displaystyle{ a = b = 2 }$ である。

$\displaystyle{ T(N) = \begin{cases} O(1) & (N = 1) \\ 2T(\frac{N}{2}) + O(N) & (N \gt 1) \end{cases} }$

よって、マージソートの計算量が $\displaystyle{ O(NlogN) }$ であることが示された。

クイックソート

指定した要素よりも小さい要素を左側に、大きい要素を右側に移動する操作を再帰的に繰り返せば、ソートされた配列が出来上がる、というコンセプト。

今まで貼ってきたGeeksforGeeksの動画の説明がわかりづらかったので別の動画も貼りました

評価

計算量: $\displaystyle{ O(NlgN) }$ 最悪 $\displaystyle{ O(N^2) }$
in-place: true
stable: false

実装例

fn quick_sort(v: &mut Vec<i32>, left: usize, right: usize) {
    // do procedure more than 3 elements exist
    if right - left < 2 {
        return
    }

    // put pivot in the middle
    let pivot_index = (left + right) / 2;
    let pivot = v[pivot_index];

    // swap pivot to the right most side
    v.swap(pivot_index, right-1);

    // seek left -> right
    let mut i = left;
    for j in left..right - 1 {
        if v[j] < pivot {
            // move smaller one to the left side
            v.swap(i, j);
            i += 1;
        }
    }
    v.swap(i, right-1);

    // after that, each elements placed like below:
    // [smaller than pivot(1)][pivot][larger than pivot(2)]
    // do procedure in (1) and (2)
    quick_sort(v, left, i);
    quick_sort(v, i+1, right);
}

クイックソートの計算量について

① 処理対象範囲を左から右へシーク: $\displaystyle{ O(N) }$

    for j in left..right - 1 {
        if v[j] < pivot {
            // move smaller one to the left side
            v.swap(i, j);
            i += 1;
        }
    }

② 分割された配列に再帰処理: $\displaystyle{ O(logN) }$

    quick_sort(v, left, i);
    quick_sort(v, i+1, right);

よって、全体としては $\displaystyle{ O(NlogN) }$ となるのが理想だが、

分割に偏りがある場合、例えば pivotとして毎回最も大きい要素、または最も小さい要素を選んでしまう場合、上記2の再帰処理の深さが $\displaystyle{ O(N) }$ となり、計算量は $\displaystyle{ O(N^2) }$ となってしまう。

乱択クイックソート

一般的に、設計したアルゴリズムの平均的な挙動について考えるとき、入力データとして考えられるものが等確率で出現するという仮定を置く。
しかし、現実には、入力分布に偏りがあったり（1 100 100 100...）、入力データ側に悪意があったり（昇順を目的としてアルゴリズムに降順のinputを与える等）する状況が考えられる。
これらの場面で有効なのか乱択化（randomization）であり、この操作を施したクイックソートを「乱択クイックソート」と呼ぶ。

配列 $\displaystyle{ a }$ の $\displaystyle{ i }$ 番目に小さい要素と、 $\displaystyle{ j }$ 番目に小さい要素（ $\displaystyle{ i \ne j }$ ）が比較されるときに1、そうでない場合に0をとる確率変数 $\displaystyle{ X_{ij} }$ を考える。

このとき、乱択クイックソートの平均計算量は

と表すことができる。

例えば、先ほどの $\displaystyle{ O(N^2) }$ となるような状況では、 $\displaystyle{ E[X_{ij}] }$ がほとんど1となる。

ここで、 $\displaystyle{ i }$ 番目の要素と、 $\displaystyle{ j }$ 番目の要素が比較される条件について考える。

要素がpivotとして選択されるよりも先に $\displaystyle{ i+1, i+2, ..., j-1 }$ 番目の要素がpivotとして選択された場合、 $\displaystyle{ i, j }$ 番目の要素はそれぞれ別の再帰関数に飛ばされてしまうので、両者が比較されることは無い。

逆に、 $\displaystyle{ i }$ または $\displaystyle{ j }$ のどちらかがpivotとして選択されれば、両者は比較される。

よって、先ほど定義した $\displaystyle{ E[X_{ij}] }$ は、 $\displaystyle{ i, i+1, ..., j-1, j }$ 番目の中で、 $\displaystyle{ i, j }$ 番目のどちらかの要素がpivotとして選択される確率を表す。

よって、 $\displaystyle{ E[X_{ij}] = \frac{2}{j-i+1} }$ となるので、

となる。以上より、乱択クイックソートの平均計算量が $\displaystyle{ O(NlogN) }$ となることが導かれた。

ここで、

\begin{align} 1 + \frac{1}{2} + \frac{1}{3} + ・・・ + \frac{1}{N} = O(logN) \end{align}

という性質を用いた。この性質は、アルゴリズムの計算量解析においてしばしば登場する。

ヒープソート

ヒープソートは、その名の通りデータ構造 ヒープ を活用する。

ヒープは最小値（または最大値）を求めるのに適した木構造の一種であり、「子要素は親要素より常に大きいか等しい（または常に小さいか等しい）」という制約を持つ。子要素が複数ある場合、子要素間の大小関係に制約はない。 https://ja.wikipedia.org/wiki/%E3%83%92%E3%83%BC%E3%83%97

与えられた配列の要素を全てヒープに挿入
ヒープの最大値を順にpopし、配列の後ろに詰める

という作業を行ってソートを実現する。

評価

計算量: $\displaystyle{ O(NlgN) }$ 最悪 $\displaystyle{ O(N^2) }$
in-place: true
stable: false

一見、ヒープを用意するために外部メモリが必要なように思われるが、ソートしたい配列自体をヒープにすることで、外部メモリを必要としない、 in-placeなアルゴリズムを実現できる。

実装例

// Heapify subtree that have the ith element as root
// target: v[0:n]
fn heapify(v: &mut Vec<i32>, i: usize, n: usize) {
    // child on the left side
    let mut child = i * 2 + 1;

    // if no child, return
    if child >= n {
        return
    }

    // compare children
    if child + 1 < n && v[child + 1] > v[child] {
        child += 1;
    }

    // if no inversion, return
    if v[child] <= v[i] {
        return
    }

    v.swap(i, child);

    heapify(v, child, n)
}

fn heap_sort(v: &mut Vec<i32>) {
    let n = v.len();

    // step 1
    // make v as Heap
    for i in (0..n/2).rev() {
        heapify(v, i, n);
    }

    // step 2
    // pop the maximum value one by one from heap
    for i in (1..n).rev() {
        v.swap(0, i);
        heapify(v, 0, i);
    }
}

余談:ソートの計算量の下界

ここまで、マージソートやヒープソートなど、計算量 $\displaystyle{ O(NlogN) }$ の様々なソートアルゴリズムを紹介した。ここでは、これらよりも高速なアルゴリズムを設計することが可能かどうかを考えてみる。

これまで見てきたソートアルゴリズムは、いずれも「ソート順序が入力要素の比較にのみ基づいて決定される」という性質のものであった。便宜的に、このようなアルゴリズムを 比較ソートアルゴリズム と呼ぶことにする。

実は、任意の比較ソートアルゴリズムにおいて、最悪の場合 $\displaystyle{ \Omega(NlogN) }$ 回の比較が必要であることを示すことができる（すなわち、マージソートやヒープソートはともに、漸近的に最良の比較ソートアルゴリズムであると言える）。証明のアイデアを以下に示す。

まず、比較ソートアルゴリズムは、大小関係の比較を繰り返すことで、最終的な順序を導く二分木としてとらえることができる。

このとき、比較ソートアルゴリズムの最悪計算量は二分木の高さ $\displaystyle{ h }$ に対応する。

要素 $\displaystyle{ N }$ の順序として考えられるものは $\displaystyle{ N! }$ 通りあるので、二分木の葉の個数は $\displaystyle{ N! }$ 必要となる。従って、

\begin{align} 2^h \ge N! \ \end{align}

を満たす必要がある。

ここで、スターリングの公式を用いる。

\begin{align} \lim_{N \to \infty} \frac{N!}{\sqrt{2\pi N} (\frac{N}{e})^N} = 1 \ \end{align}

スターリングの公式は階乗 $\displaystyle{ n! }$ を指数関数で近似する公式です。統計力学（物理の一分野）や組み合わせ数学で用いられます。階乗よりも指数関数の方が扱いやすい場合が多いので嬉しいです。 https://manabitimes.jp/math/763

これによって、

\begin{align} log_eN! \simeq Nlog_eN-N+ \frac{1}{2}log_e(2 \pi N) \end{align}

が成立し、

\begin{align} log_eN! = \Theta(NlogN) \end{align}

$\displaystyle{ \Theta }$ について $\displaystyle{ f(n)=\Theta(g(n)) }$ の時、十分大きな $\displaystyle{ n }$ について、定数倍を無視すれば $\displaystyle{ f(n) }$ の値は $\displaystyle{ g(n) }$ が上限にも下限にもなることを意味する。 https://algo-logic.info/asymptotic-analysis/#toc_id_3_2

であることが言える。

ここで、

\begin{align} h \ge log_2(N!) \gt log_e(N!) \end{align}

より、

\begin{align} h = \Omega(NlogN) \end{align}

が成立する。以上から、任意の比較ソートアルゴリズムは、最悪の場合、 $\displaystyle{ Omega(NlogN) }$ 回の比較が必要であることが示された。

分布数え上げソート（Countingソート）

先ほど、 $\displaystyle{ O(NlogN) }$ の計算量を持つマージソートやヒープソートが、漸近的に最速な比較ソートアルゴリズムであることを確認した。比較ソートアルゴリズムである限り、定数倍の違いを除いて、これらより早いものは存在しないと言える。

ここで紹介する 分布数え上げソート（Countingソート） は比較ソートアルゴリズムではないソートアルゴリズムである。

分布数え上げソートはソート対象のデータをキーにして、キーの出現回数とその累積度数分布を計算して利用することで整列を行うアルゴリズムです。キーとなるデータがとりうる値の範囲をあらかじめ知っている必要があります。 https://www.codereading.com/algo_and_ds/algo/counting_sort.html

評価

計算量: $\displaystyle{ O(N + A) }$ （配列の要素 $\displaystyle{ x }$ が $\displaystyle{ 0 \le x \lt A }$ である場合）
in-place: false
stable: true

実装例

// on the assumption that each elements is less than 100000
const MAX: usize = 100000;

fn main() {
    let mut v = vec![3,6,2,154,5,41,564,21,86,9];
    assert_eq!(counting_sort(&mut v), vec![2, 3, 5, 6, 9, 21, 41, 86, 154, 564]);
}

fn counting_sort(v: &mut Vec<i32>) -> Vec<i32> {
    let n = v.len();

    // count each elements
    let mut num = vec![0; MAX];
    for i in 0..n {
        num[v[i] as usize] += 1
    }

    // get cumulative sum of num
    let mut sum = vec![0; MAX];
    for value in 1..MAX {
        sum[value] = sum[value-1] + num[value];
    }

    let mut v2: Vec<i32> = vec![0; n];
    for i in (0..n).rev() {
        v2[sum[v[i] as usize] - 1] = v[i];
    }
    v2
}

まとめ

比較型のソートアルゴリズムと、そうでないアルゴリズムがある。前者は $\displaystyle{ O(NlogN) }$ が最速。
ソートは時間計算量、in-place性、安定性の観点から評価することができる。

お世話になった本

問題解決力を鍛える！アルゴリズムとデータ構造 (ＫＳ情報科学専門書) | 大槻兼資, 秋葉拓哉 | 工学 | Kindleストア | Amazon

登場したアルゴリズムたち

KenchonBook/chapter12/src at main · kubosuke/KenchonBook · GitHub

2021-11-13

ARC101 D Median of Medians

問題

https://atcoder.jp/contests/arc101/tasks/arc101_b

定義

$\displaystyle{ b }$ を昇順にソートして得られる数列を $\displaystyle{ b′ }$ とする。このとき、 $\displaystyle{ b′ }$ の $\displaystyle{ \frac{M}{2}+1 }$ 番目の要素の値を、b の中央値とする。ここで、/ は小数点以下を切り捨てる除算である。

解法

$\displaystyle{ f(X) = }$ 求める中央値が $\displaystyle{X}$ 以下となるかどうか

という判定条件を考える。

この判定条件が初めてtrueになる境界を二分探索で求めていく。

与えられる数列 $\displaystyle{ a }$ の区間 $\displaystyle{ [l,r) }$ は、 $\displaystyle{ a }$ の長さを $\displaystyle{ M }$ とおくと、 $\displaystyle{ _{M+1}C_2 }$ 個ある。

例) $\displaystyle{ [30,10,20] }$ の区間は、 $\displaystyle{ [[30], [10], [20], [30, 10], [10, 20], [30, 10, 20]] }$ の $\displaystyle{ _{3+1}C_2 }$ = 6通り

「考えられうる区間の半数」以上、すなわち「 $\displaystyle{ \frac{_{M+1}C_2}{2} }$ 個以上の区間」の中央値が $\displaystyle{ X }$ 以下であれば、 $\displaystyle{ f(X) = true }$ となる。

「区間の中央値が $\displaystyle{ X }$ 以下がどうか」は、特に区間をsortせずとも、

$\displaystyle{ X }$ 以上の要素を1, $\displaystyle{ X }$ 未満の要素を-1に変換
区間の総和が0未満となるかどうか

で判定できる。

区間の総和は、累積和を使うと処理しやすい。

$\displaystyle{ S_0 }$ = 0
$\displaystyle{ S_1 }$ = $\displaystyle{ a_0 }$
$\displaystyle{ S_2 }$ = $\displaystyle{ a_0 + a_1 }$
$\displaystyle{ S_3 }$ = $\displaystyle{ a_0 + a_1 + a_2 }$

とおくと、区間 $\displaystyle{ [l, r) }$ の総和は $\displaystyle{ S_r - S_l }$ と求めることができる。

よって、問題は次のように言い換えることができる。

数列 $\displaystyle{ a }$ の要素のうち、 $\displaystyle{ x }$ 以上の要素を $\displaystyle{ 1 }$ 、 $\displaystyle{ x }$ 未満の要素を $\displaystyle{ -1 }$ へと変換した数列を $\displaystyle{ b }$ とおく。
$\displaystyle{ b }$ の累積和数列 $\displaystyle{ S }$ において、 $\displaystyle{ S_r - S_l \lt 0 }$ となる区間 $\displaystyle{ [l, r) }$ の数が $\displaystyle{ \frac{_{M+1}C_2}{2} }$ 以上であるような、最小の $\displaystyle{ x }$ を求めよ。

ここで、

$\displaystyle{ S }$ において、 $\displaystyle{ S_r - S_l \lt 0 }$ となる区間 $\displaystyle{ [l, r) }$ の数

は、 $\displaystyle{ S }$ の転倒数を求めていることとほぼ同義である。

ここの転倒数を求める処理で、愚直に

        for l in 0..n as usize {
            for r in l..n as usize {
                if S[r] < S[l] {
                    cnt += 1
                }
            }
        }

とすると、 $\displaystyle{ O(N^2) }$ となり、実行時間切れとなる。 Fenwick Tree等を用いて、 $\displaystyle{ O(Nlog(N)) }$ あたりまで計算量を下げることが求められる。

Fenwick Treeを用いた転倒数算出については別エントリに記載した。

// https://atcoder.jp/contests/arc101/tasks/arc101_b

use proconio::input;

// nearly exceeds 10^9
const A_MAX: i64 = 1<<30;

struct Fenwick {
    tree: Vec<i64>,
}

impl Fenwick {
    /// create Fenwick Tree by given length
    pub fn new(len: usize) -> Self {
        Self { tree: vec![0; len] }
    }

    /// add `w` to index `i`
    /// `i` is 1-indexed
    pub fn add(&mut self, mut i: usize, w: i64) {
        while i < self.tree.len() {
            self.tree[i] += w;
            i += lsb(i);
        }
    }

    /// sum `[1, a]`
    /// `a` is 1-indexed
    pub fn sum(&self, mut i: usize) -> i64 {
        let mut res = 0;
        while i > 0 {
            res += self.tree[i];
            i -= lsb(i);
        }
        res
    }

    /// sum `[a, b)`
    /// a and b are 1-indexed
    pub fn partial_sum(&self, a: usize, b: usize) -> i64 {
        self.sum(b-1) - self.sum(a-1)
    }
}

/// return least significant bit of i
fn lsb(i: usize) -> usize {
    if i == 0 {
        0
    } else {
        i & !(i - 1)
    }
}

fn main() {
    input! {
        n: i64,
        mut a: [i64; n]
    }

    if n == 1 {
        println!("{}", a[0]);
        return
    }

    let mut left = 0;
    let mut right = A_MAX;
    let geta = n + 1;
    while right - left > 1 {
        let mid = (right + left) / 2;
        let mut inversion_number = 0;
        let mut ft = Fenwick::new(n as usize * 2 + 10);
        let mut sum = 0;
        ft.add((sum + geta) as usize, 1);
        for i in 0..n as usize {
            let val = if a[i] <= mid { 1 } else { -1 };
            sum += val;
            inversion_number += ft.partial_sum(1, (sum+geta) as usize);
            ft.add((sum+geta) as usize, 1);
        }

        if inversion_number as i64 > (n+1)*n/2/2 {
            right = mid;
        } else {
            left = mid;
        }
    }
    println!("{}", right);
}

references

2021-11-12

Fenwick Tree(Binary Indexed Tree) で Inversion Number(転倒数) を求める

Inversion Number とは

https://en.wikipedia.org/wiki/Inversion_(discrete_mathematics)

$\displaystyle{ i \lt j }$ において、 $\displaystyle{ a_i \gt a_j }$ となるペアの数の総和。要は、右より左の値の方が大きいペアの数の総和。数列の整列性の指標などに用いられる。

Fenwick Tree とは

ある配列 $\displaystyle{ a }$ について、

$\displaystyle{ a_i }$ に $\displaystyle{ x }$ を加算する
$\displaystyle{ \sum_{x=i}^{j} a_x }$ を計算する

これらの処理を $\displaystyle{ O(logN) }$ で計算できるデータ構造。ある区間の総和も、ある要素への加算も、速く計算したいという用途で威力を発揮する。

実態は $\displaystyle{ len(a) + 1 }$ のノードを持つ木構造。根を除くそれぞれのノードは、 $\displaystyle{ [a,b) }$ の区間の総和を管理する。

f:id:twosec:20211112210900p:plain

どのように数列の値を木へセットしていくか
どのように親のノードの番号を求めるか
どのようにノードの値を更新するか

この辺りは Tushar Royさんの Coding Made Simple - Fenwick Tree or Binary Indexed Tree がとても分かりやすい。割愛する。

Inversion Number の算出方法

ナイーブな実装

愚直に計算する場合、

        let mut res = 0;
        for l in 0..n-1 as usize {
            for r in l+1..n as usize {
                if a[r] < a[l] {
                    res += 1
                }
            }
        }

$\displaystyle{ O(N^2) }$ の処理となる。

Fenwick Tree を用いた実装

まず、それぞれのノードに、 $\displaystyle{ [a,b) }$ の区間に含まれる（a以上b未満である）数列の要素数を管理させることを考える。

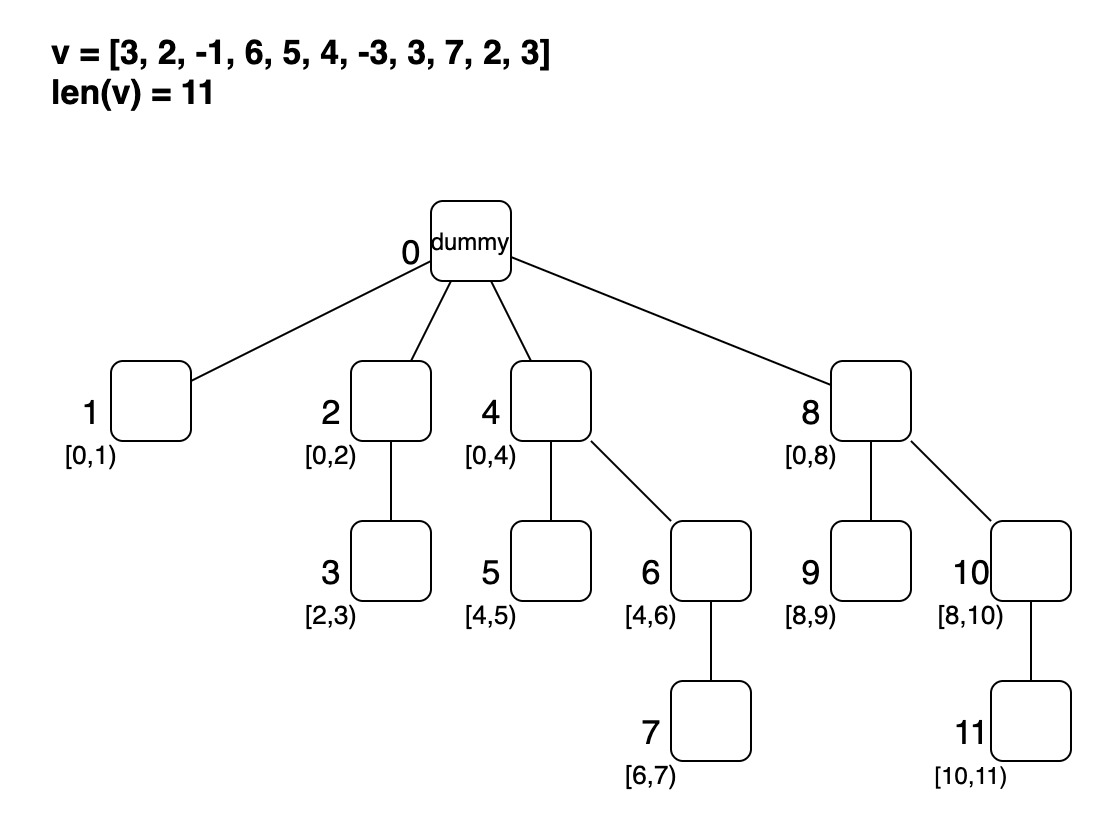
例として、 $\displaystyle{ a = [2,1,5,4,3] }$ という数列を考える。 $\displaystyle{ a_i = 4 }$ $\displaystyle{ (i = 0,1,2,3) }$ までセットした結果は次のようになる。

f:id:twosec:20211112210949p:plain

次の要素 $\displaystyle{ a_i = 3(i = 4) }$ よりも左にあり、値が大きい数をどのように求めるか。

前述の通り、Fenwick Treeは $\displaystyle{ \sum_{x=i}^{j} a_x }$ のような計算が得意だ。 $\displaystyle{ [0,3) }$ の区間に存在する要素数は、index = 3のノードから、根までの総和によって求めることができる。

f:id:twosec:20211112211000p:plain

このとき、自分（ $\displaystyle{ a_i = 3 }$ ）よりも左にあって、自分よりも値が大きい数は、（今まで登録した要素の数） - （ $\displaystyle{ [0,3) }$ の区間に存在する要素数） = 4 - 2 = 2 (5と4)

となる。

これを全ての要素に対して計算して総和を求めれば、inversion numberとなる。

計算量は、

自分よりも左にあって、自分よりも値が大きい数の算出:
- これを全ての要素に対して行う: $\displaystyle{ O(Nlog(N)) }$
Fenwick Treeに値をセットする操作: $\displaystyle{ O(log(N)) }$

より、 $\displaystyle{ O(Nlog(N)) }$ によって求めることができる。

use std::fmt;

struct Fenwick {
    tree: Vec<i32>,
}

impl Fenwick {
    /// Constructs a new fenwick tree with the specified `len`
    ///
    /// # Examples
    ///
    /// ```
    /// let f = Fenwick::new(5);
    /// ```
    pub fn new(len: usize) -> Self {
        Self { tree: vec![0; len] }
    }

    /// Update the value at `i` by `w`.
    ///
    /// Complexity: _O_(log_n_).
    pub fn add(&mut self, mut i: usize, w: i32) {
        i += 1;
        while i < self.tree.len() {
            self.tree[i] += w;
            i += lsb(i);
        }
    }

    /// Get a partial sum from 0 to `i`.
    ///
    /// Complexity: _O_(log_n_).
    pub fn sum(&self, mut i: usize) -> i32 {
        let mut res = 0;
        while i != 0 {
            res += self.tree[i];
            i -= lsb(i);
        }
        res
    }
}

impl fmt::Debug for Fenwick {
    fn fmt(&self, f: &mut fmt::Formatter<'_>) -> fmt::Result {
        f.debug_struct("Fenwick")
            .field("tree", &self.tree)
            .finish()
    }
}

/// return least significant bit of i
///
/// # Examples
///
/// ```
/// let x1 = lsb(8);
/// let x2 = lsb(10);
/// let x3 = lsb(24);
/// assert_eq!(8, x1)
/// assert_eq!(2, x2)
/// assert_eq!(8, x3)
/// ```
fn lsb(i: usize) -> usize {
    if i == 0 {
        0
    } else {
        i & !(i - 1)
    }
}

fn main() {
    let v = vec![2,1,5,4,3];

    let mut b = Fenwick::new(v.len()+1);
    let mut ans = 0;
    let mut i = 0;
    while i < v.len() {
        ans += (i+1) - b.sum(v[i])  as usize - 1;
        b.add(v[i], 1);
        i += 1;
    }

    assert_eq!(4, ans);
}

ノード $\displaystyle{ x }$ を更新したときに、波及して更新する必要のあるノード番号は、

$\displaystyle{ y = }$ 2's complement of $\displaystyle{ x }$
$\displaystyle{ z = x }$ AND $\displaystyle{ y }$
$\displaystyle{ x + z }$

によって求めることができる。

同様に、ノード $\displaystyle{ x }$ の親ノード番号は、

$\displaystyle{ y = }$ 2's complement of $\displaystyle{ x }$
$\displaystyle{ z = x }$ AND $\displaystyle{ y }$
$\displaystyle{ x - z }$

によって求めることができる。

$\displaystyle{ z }$ は、least significant bit または right most set bit と呼ばれ、「引数を割り切る最大の2冪」を意味する。

$\displaystyle{ z }$ は、 $\displaystyle{ i-1 }$ と $\displaystyle{ -i }$ がbit反転の関係にあることより、以下のように求めることができる。

fn lsb(i: usize) -> usize {
    if i == 0 {
        0
    } else {
        i & !(i - 1)
    }
}

参考

このエントリと同じテーマ。: https://iq.opengenus.org/count-inversions-in-an-array-using-fenwick-tree/
このエントリと同じテーマ。: https://scrapbox.io/pocala-kyopro/%E8%BB%A2%E5%80%92%E6%95%B0
Fenwickさんの論文。: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.14.8917&rep=rep1&type=pdf
ngtkanaさんのrustによるBIT実装、解説。: https://qiita.com/ngtkana/items/7d50ff180a4e5c294cb7#comment-100c04e7fa7a913ce276
Fenwick Treeが更新されていく手順。: https://youtu.be/CWDQJGaN1gY

2021-10-24

ARC037 C 億マス計算

問題

https://atcoder.jp/contests/arc037/tasks/arc037_c

解法

まずはナイーブに全探索を実装することを考える。

// https://atcoder.jp/contests/arc037/tasks/arc037_c

use proconio::input;

fn main() {
    input! {
        n: i64,
        k: i64,
        mut a: [i64; n],
        mut b: [i64; n],
    }
    let mut x = vec![];
    for aa in &a {
        for bb in &b {
            x.push(aa*bb)
        }
    }
    x.sort();
    println!("{}", x[(k-1) as usize])
}

この場合、次のような計算量となる。

行列を配列xに平坦化する処理: O(n²)
平坦化した配列xをソートする処理: O(n² logn)

1 ≦ N ≦ 30000 であるため、この計算量だと 10⁸ を若干超えてしまう。リソースの乏しいジャッジサーバの悲痛な叫びが聞こえてくる、そんな数字だ。 1812年のロシア遠征で無謀な行軍をしたナポレオンのように、一か八かの賭けに臣下を巻き添えにしてはならない。我々は領土欲、名誉欲に眩んだとしても、決して綱渡り的遠征、綱渡り的全探索など行うべきではないのだ。

どのように計算量を削減するか。「x番目の最小値 / 最大値」を求める問題は、二分探索によって効率的に求めることができる。

すなわち、本問題を「 N² 個の整数のうち、K番目に小さい値を求める」 => 「 N² 個の整数のうち、値が x 以下となる整数の個数が K となるような x の最小値を求める」と言い換えて考える。（x以下となる整数の数がK以上となるxの最小値 = 数がKとなる上限 = 小さい方からK番目の数）

// https://atcoder.jp/contests/arc037/tasks/arc037_c

use proconio::input;

const INF: i64 = 1<<60;

fn check(a: &Vec<i64>, b: &Vec<i64>, x: i64, k: usize) -> bool {
    let mut cnt = 0;
    let mut j = 0;
    for a in a.iter().rev() {
        while j < b.len() && *a * b[j] <= x {
            j += 1;
        }
        cnt += j;
    }
    return cnt >= k
}

fn main() {
    input! {
        n: i64,
        k: i64,
        mut a: [i64; n],
        mut b: [i64; n],
    }
    a.sort();
    b.sort();

    let mut left = 0;
    let mut right = INF;

    // 'k' th minimum value
    // => minimum x | the number of value that satisfy < x is K in []a*b
    // in this case, x is the upper bound of []a*b which satisfy 'k' th minimum value
    while right - left > 1 {
        let mid = (left + right) / 2;
        if check(&a, &b, mid, k as usize) {
            right = mid
        } else {
            left = mid
        }
    }
    println!("{}", right)
}

二分探索、という言葉を字句通り受け取れば、単なる中間値を参照・比較して目的の値を見つける探索手段のように思えるが、実は「**となる上限/下限の最小値/最大値を求める」ことで目的の解を得るというロジック、これこそに、この探索法のエッセンスが詰まっていると僕は思う。