Inversion Number とは

https://en.wikipedia.org/wiki/Inversion_(discrete_mathematics)

$\displaystyle{ i \lt j }$ において、 $\displaystyle{ a_i \gt a_j }$ となるペアの数の総和。要は、右より左の値の方が大きいペアの数の総和。数列の整列性の指標などに用いられる。

Fenwick Tree とは

ある配列 $\displaystyle{ a }$ について、

$\displaystyle{ a_i }$ に $\displaystyle{ x }$ を加算する
$\displaystyle{ \sum_{x=i}^{j} a_x }$ を計算する

これらの処理を $\displaystyle{ O(logN) }$ で計算できるデータ構造。ある区間の総和も、ある要素への加算も、速く計算したいという用途で威力を発揮する。

実態は $\displaystyle{ len(a) + 1 }$ のノードを持つ木構造。根を除くそれぞれのノードは、 $\displaystyle{ [a,b) }$ の区間の総和を管理する。

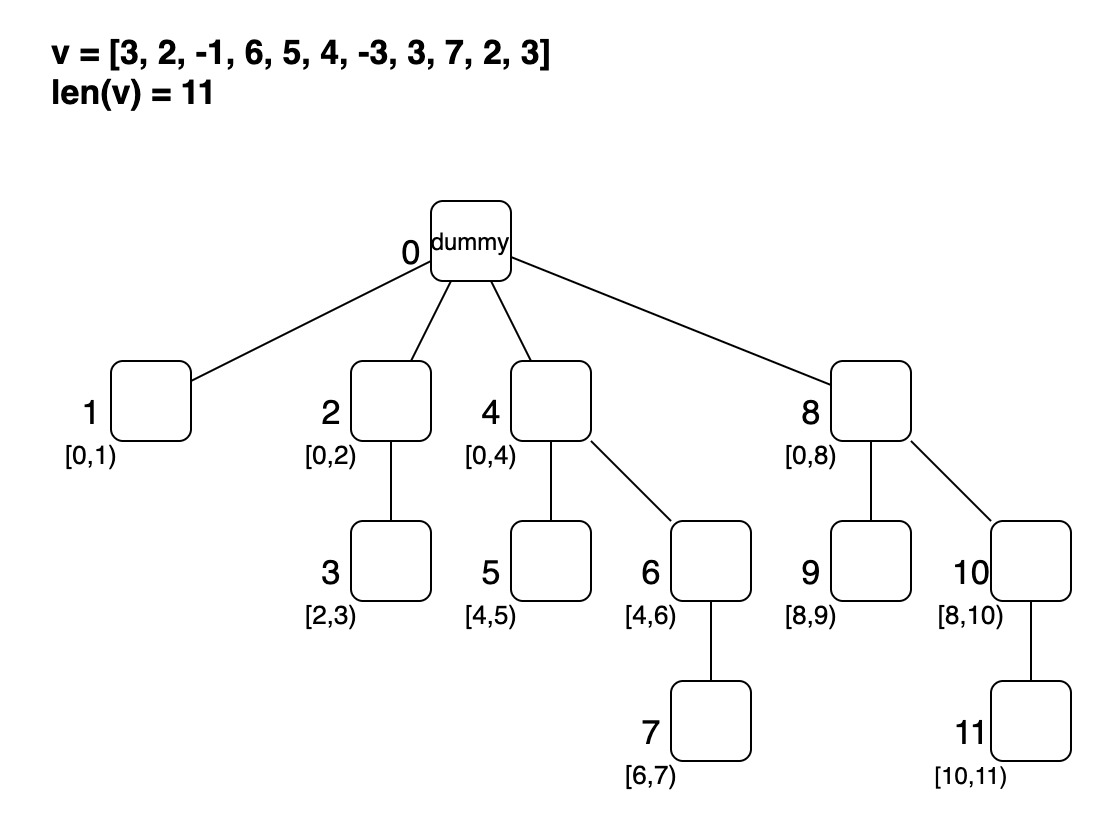
f:id:twosec:20211112210900p:plain

どのように数列の値を木へセットしていくか
どのように親のノードの番号を求めるか
どのようにノードの値を更新するか

この辺りは Tushar Royさんの Coding Made Simple - Fenwick Tree or Binary Indexed Tree がとても分かりやすい。割愛する。

Inversion Number の算出方法

ナイーブな実装

愚直に計算する場合、

        let mut res = 0;
        for l in 0..n-1 as usize {
            for r in l+1..n as usize {
                if a[r] < a[l] {
                    res += 1
                }
            }
        }

$\displaystyle{ O(N^2) }$ の処理となる。

Fenwick Tree を用いた実装

まず、それぞれのノードに、 $\displaystyle{ [a,b) }$ の区間に含まれる（a以上b未満である）数列の要素数を管理させることを考える。

例として、 $\displaystyle{ a = [2,1,5,4,3] }$ という数列を考える。 $\displaystyle{ a_i = 4 }$ $\displaystyle{ (i = 0,1,2,3) }$ までセットした結果は次のようになる。

f:id:twosec:20211112210949p:plain

次の要素 $\displaystyle{ a_i = 3(i = 4) }$ よりも左にあり、値が大きい数をどのように求めるか。

前述の通り、Fenwick Treeは $\displaystyle{ \sum_{x=i}^{j} a_x }$ のような計算が得意だ。 $\displaystyle{ [0,3) }$ の区間に存在する要素数は、index = 3のノードから、根までの総和によって求めることができる。

f:id:twosec:20211112211000p:plain

このとき、自分（ $\displaystyle{ a_i = 3 }$ ）よりも左にあって、自分よりも値が大きい数は、（今まで登録した要素の数） - （ $\displaystyle{ [0,3) }$ の区間に存在する要素数） = 4 - 2 = 2 (5と4)

となる。

これを全ての要素に対して計算して総和を求めれば、inversion numberとなる。

計算量は、

自分よりも左にあって、自分よりも値が大きい数の算出:
- これを全ての要素に対して行う: $\displaystyle{ O(Nlog(N)) }$
Fenwick Treeに値をセットする操作: $\displaystyle{ O(log(N)) }$

より、 $\displaystyle{ O(Nlog(N)) }$ によって求めることができる。

use std::fmt;

struct Fenwick {
    tree: Vec<i32>,
}

impl Fenwick {
    /// Constructs a new fenwick tree with the specified `len`
    ///
    /// # Examples
    ///
    /// ```
    /// let f = Fenwick::new(5);
    /// ```
    pub fn new(len: usize) -> Self {
        Self { tree: vec![0; len] }
    }

    /// Update the value at `i` by `w`.
    ///
    /// Complexity: _O_(log_n_).
    pub fn add(&mut self, mut i: usize, w: i32) {
        i += 1;
        while i < self.tree.len() {
            self.tree[i] += w;
            i += lsb(i);
        }
    }

    /// Get a partial sum from 0 to `i`.
    ///
    /// Complexity: _O_(log_n_).
    pub fn sum(&self, mut i: usize) -> i32 {
        let mut res = 0;
        while i != 0 {
            res += self.tree[i];
            i -= lsb(i);
        }
        res
    }
}

impl fmt::Debug for Fenwick {
    fn fmt(&self, f: &mut fmt::Formatter<'_>) -> fmt::Result {
        f.debug_struct("Fenwick")
            .field("tree", &self.tree)
            .finish()
    }
}

/// return least significant bit of i
///
/// # Examples
///
/// ```
/// let x1 = lsb(8);
/// let x2 = lsb(10);
/// let x3 = lsb(24);
/// assert_eq!(8, x1)
/// assert_eq!(2, x2)
/// assert_eq!(8, x3)
/// ```
fn lsb(i: usize) -> usize {
    if i == 0 {
        0
    } else {
        i & !(i - 1)
    }
}

fn main() {
    let v = vec![2,1,5,4,3];

    let mut b = Fenwick::new(v.len()+1);
    let mut ans = 0;
    let mut i = 0;
    while i < v.len() {
        ans += (i+1) - b.sum(v[i])  as usize - 1;
        b.add(v[i], 1);
        i += 1;
    }

    assert_eq!(4, ans);
}

ノード $\displaystyle{ x }$ を更新したときに、波及して更新する必要のあるノード番号は、

$\displaystyle{ y = }$ 2's complement of $\displaystyle{ x }$
$\displaystyle{ z = x }$ AND $\displaystyle{ y }$
$\displaystyle{ x + z }$

によって求めることができる。

同様に、ノード $\displaystyle{ x }$ の親ノード番号は、

$\displaystyle{ y = }$ 2's complement of $\displaystyle{ x }$
$\displaystyle{ z = x }$ AND $\displaystyle{ y }$
$\displaystyle{ x - z }$

によって求めることができる。

$\displaystyle{ z }$ は、least significant bit または right most set bit と呼ばれ、「引数を割り切る最大の2冪」を意味する。

$\displaystyle{ z }$ は、 $\displaystyle{ i-1 }$ と $\displaystyle{ -i }$ がbit反転の関係にあることより、以下のように求めることができる。

fn lsb(i: usize) -> usize {
    if i == 0 {
        0
    } else {
        i & !(i - 1)
    }
}

参考

このエントリと同じテーマ。: https://iq.opengenus.org/count-inversions-in-an-array-using-fenwick-tree/
このエントリと同じテーマ。: https://scrapbox.io/pocala-kyopro/%E8%BB%A2%E5%80%92%E6%95%B0
Fenwickさんの論文。: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.14.8917&rep=rep1&type=pdf
ngtkanaさんのrustによるBIT実装、解説。: https://qiita.com/ngtkana/items/7d50ff180a4e5c294cb7#comment-100c04e7fa7a913ce276
Fenwick Treeが更新されていく手順。: https://youtu.be/CWDQJGaN1gY

2sec

2秒間でライムを刻め

Fenwick Tree(Binary Indexed Tree) で Inversion Number(転倒数) を求める

Inversion Number とは

Fenwick Tree とは

Inversion Number の算出方法

ナイーブな実装

Fenwick Tree を用いた実装

参考